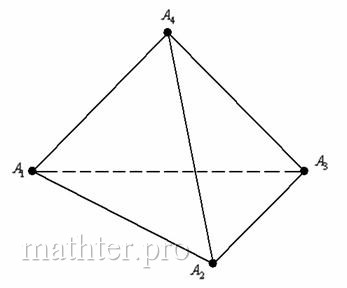
Боковое ребро правильной пирамиды, формула
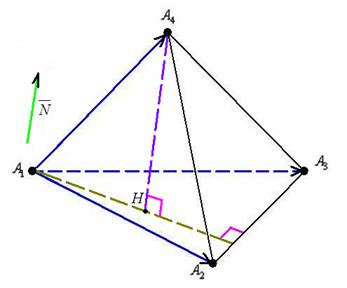
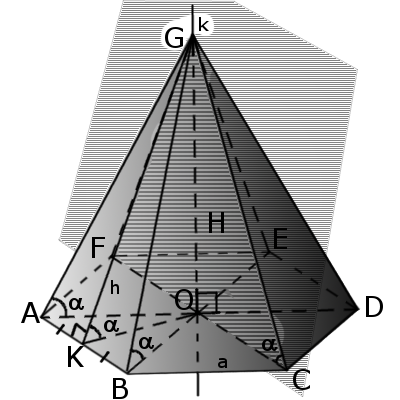
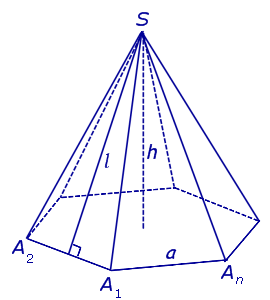
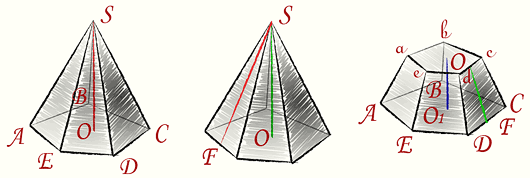
Высота этих треугольников, проведенная из вершины пирамиды, называется апофемой. Найдите объем пирамиды. Так как пирамида правильная, то высота падает в центр основания, то есть в точку пересечения медиан высот, биссектрис.
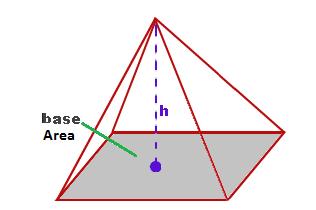
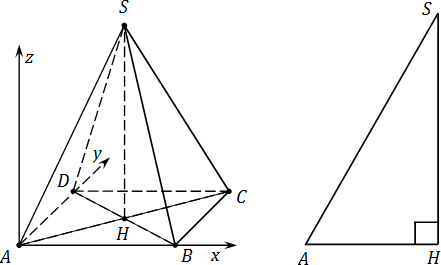

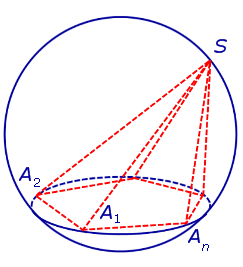


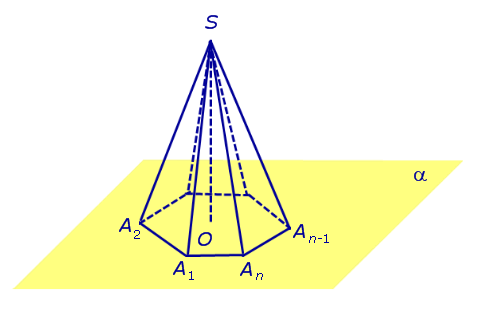



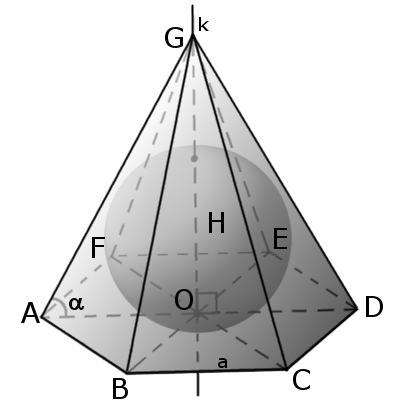
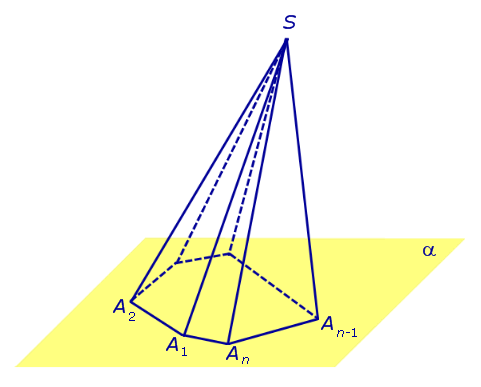
Рассмотрим правильную n -угольную пирамиду. Этот многогранник часто встречается в стереометрических задачах, и поэтому более подробное и тщательное изучение его свойств представляет большой интерес. В этом параграфе мы несколько расширим тот арсенал формул, который нами был получен ранее.
- Регистрация Вход.
- Справочник по математике Геометрия Стереометрия Пирамиды. Пирамидой n - угольной пирамидой называют фигуру, образованную отрезками, соединяющими точку S со всеми точками многоугольника A 1 A
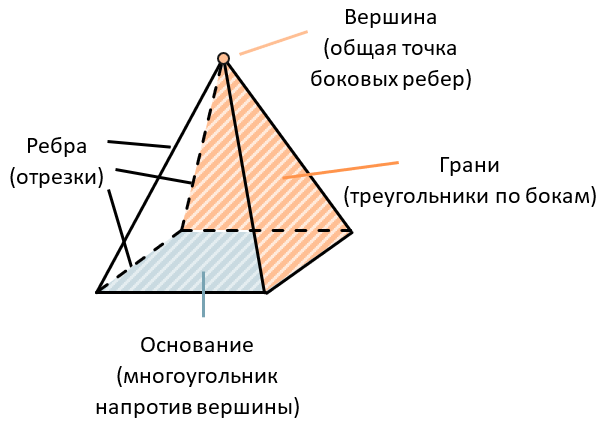
- Пирамидой называют многогранник, одна грань которого — многоугольник, а остальные грани — треугольники с общей вершиной.
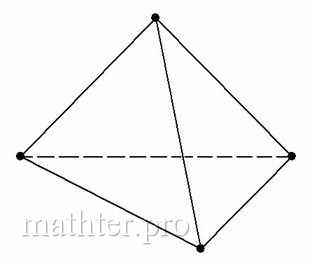
- В этом уроке приведены определение и свойства правильной треугольной пирамиды и ее частного случая - тетраэдра см. Ссылки на примеры решения задач приведены в конце урока.
- Высшая математика — просто и доступно! Математические формулы, таблицы и другие материалы.
- Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
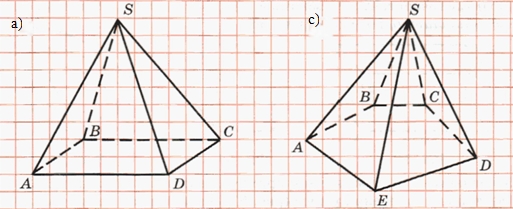


Определение: Параллелепипед — это призма, основания которой параллелограммы. В этом определении ключевым словом является «призма». Таким образом, параллелепипед — это частный случай призмы, которая отличается от общего случая только тем, что в основании у нее не произвольный многоугольник, а именно параллелограмм. Поэтому все приведенные выше свойства, формулы и определения касающиеся призмы остаются актуальными и для параллелепипеда. Однако, можно выделить несколько дополнительных свойств характерных для параллелепипеда.